
As such, an estimator of the standard deviation is s = R/d 2. The mean and standard deviation of W is d 2 and d 3. The parameters of the distribution of W (mean and standard deviation) are a function of the sample size n. We call this variable (W) the Relative Range. We can describe that relationship as a random variable W = R / σ. In statistics, there is a relationship between the range of a sample, from a normal distribution, and the standard deviation of that distribution. R = x max – x min This next part is critical! 2.0 Computing d 2 and d 3 using the Relative Range, W To compute the range, we take the difference between the largest and smallest value as shown in the expression below. Let’s say that x 1, x 2,…, x n describes a single value, of a part feature, from n samples. Let’s talk about the basics… 1.0 Computing the Range In this article, I’ll focus on the range method and illustrate how we can derive the constants: d 2, d 3, D 3 and D 4 used to compute the control limits for a Range chart. To estimate the standard deviation (σ) we compute the average Range across m subgroups and divide by a correction factor, called d 2. The Range is the smallest value subtracted from the largest value in a subgroup. As such, the data that describes a feature derived from n like samples estimates common cause variation.įor each subgroup we compute the range and plot those values on the Range chart. Doing so assures the conditions that produced the first sample are likely the same for the remaining n-1 samples. To assure we collect n samples made under like conditions, we collect consecutive samples over a short period of time. Each subgroup is a collection of n samples made under like conditions. We can estimate σ from m subgroups taken from a process. To build control limits for a Range chart we need to estimate the standard deviation, σ. After you go through this article, you’ll be building Xbar and R charts with ease and confidence! It all starts with this chart… The Range Chart Knowing where these constants come from and how you can derive them through simple simulations will improve your knowledge and deepen your appreciation of statistical process control.
#Xbar and ybar formula how to
I’ll also show you how to use them to compute control limits for the Xbar and R chart. In this article, I’ll show you how to derive the following constants: d 2, d 3, A 2, D 3, and D 4. And, while the control chart constants used to compute control limits appears to be a mystery, they are quite easy to understand and derive.
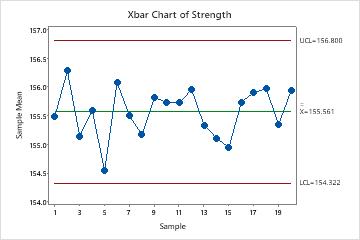
The truth is computing control limits isn’t that complicated. I know I did! I recall looking up values for A 2 and D 4 without any idea where they came from. But, have you ever wondered how these control limits for an Xbar and R chart were computed?įor those of you that had to perform the calculations by hand, chances are you applied Xbar and R chart formulas using various control chart constants.
#Xbar and ybar formula software
To estimate the mean and total of y-values, denoted as \(\mu\) and \(\tau\), one can use the linear relationship between y and known x-values.If so, you most likely used some type of software package to display your data and compute the necessary control limits for your Xbar and R chart. In addition, if multiple auxiliary variables have a linear relationship with y, multiple regression estimates may be appropriate. The two estimates, regression, and ratio may be quite close in such cases and you can choose the one you want to use. This does not mean that the regression estimate cannot be used when the intercept is close to zero. When the auxiliary variable x is linearly related to y but does not pass through the origin, a linear regression estimator would be appropriate. Looking at the data, how will we find things that will work, or which model should we use? These are key questions. The variance for the estimators will be an important indicator.


 0 kommentar(er)
0 kommentar(er)
